McGill
 Frustrated Magnets Group
µSR Page


We are currently using µSR to study the static and dynamic behaviour of magnetic order in partially frustrated magnetic materials.

The experimental work takes place in the Meson Hall
at TRIUMF in Vancouver, BC.

µ+ are produced through the decay of pi+ created by proton bombardment of a graphite target. They are collected and implanted into our sample. The subsequent decay positron (e+) is detected in one of four scintillation counters placed in the forward, backward, left and right directions relative to the incoming beam. The forward and backward detectors are visible at the left and right of the picture (pairs of cylinders attached to the black plates). The (similar) muon arrival detector is also visible at the lower left. The central structure is the cryostat containing our sample, and surrounded by (red) Helmholtz coils to control the magnetic field at the sample.
We have made measurements using two different beam-lines.

M13
M20
Data collection

The actual data-taking process is of course an extremely complex process that can only be undertaken by highly-trained µSR specialists.
The intense concentration required is demonstrated here by Prof. J.M. Cadogan (UNSW) and J. van Lierop (McGill).


Introduction
Muons can be used to probe magnetic order because:
(i) they have a magnetic moment
(ii) the positron produced when the muon decays is emitted preferentially in the direction that the muon moment is pointing.
By implanting muons with a known initial moment direction (the surface muon beam at TRIUMF is almost 100% polarised with the muon moments pointing anti-parallel to the flight direction i.e. backwards) and measuring the ratio between positrons detected in the forward and backward directions (the `asymmetry') as a function of time, changes in the muon moment direction can be observed.

Raw data for silver in a field of 4 mT

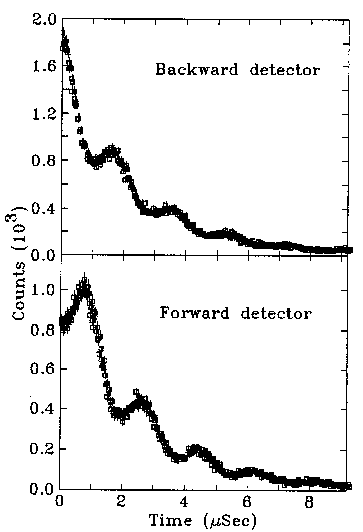
The strongest time dependence comes from the 2.2µs lifetime of the muon, however the data also show an oscillating component. Comparing the upper and lower panels reveals that when the forward detector shows a maximum, the backward detector has a minimum. The muons are precessing in the 4 mT vertical field and the decay positrons form a beam that turns with them.

Asymmetry data for silver in a field of 4 mT

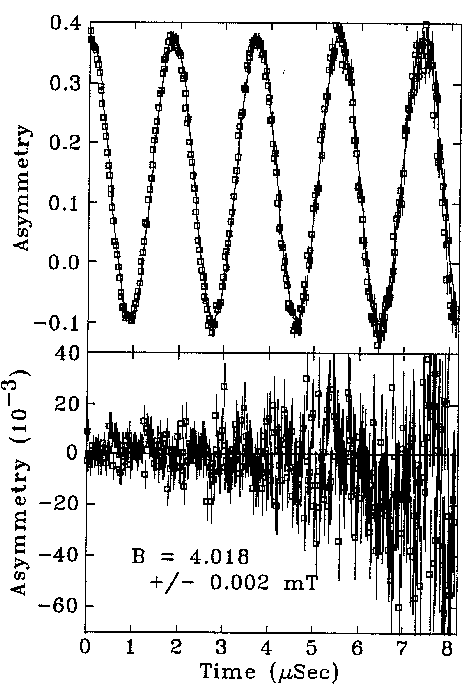By calculating the asymmetry (F-B)/(F+B) the exponential decay of the muons can be scaled out, leaving only the precession. The period of the sinusoidal variation can be determined by fitting, and knowing the gyromagnetic ratio (135 MHz/T) the field experienced by the muons can be calculated.

Application to the study of transverse spin freezing in partially frustrated ferromagnets.


While the detailed situation in the samples we are studying is more complex, the underlying behaviour is unchanged. Our samples are both structurally and magnetically disordered, so rather than seeing a single unique field, the implanted muons are subject to fields that are distributed in both magnitude and direction. This washes out the simple precession seen above in silver and leads to a form with a single minimum. The position of this minimum is related to the average field at the muon implantation sites. A typical curve is shown in the inset below.

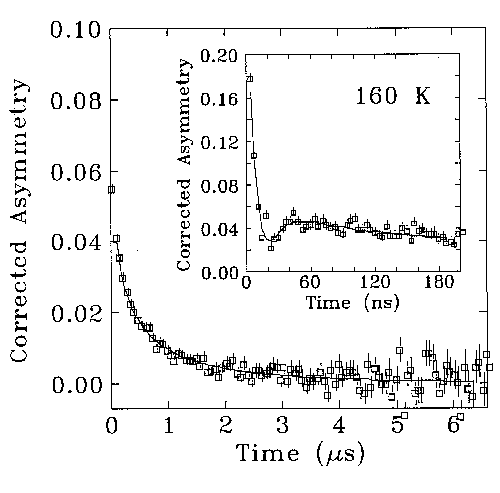If the muons are also subjected to magnetic fields that vary in time, then the muon moment directions will be randomised at a rate that depends on these field fluctuations. An exponential decay in the asymmetry is observed (see main picture above).

For our purposes, muons provide two main advantages:
(i) The measurements are made with no externally applied field that might modify the magnetic properties
(ii) Static and time-dependent phenomena are fully distinguished in the data.
This last point can be confirmed by looking at the picture shown above. The static minumum (inset) occurs around 40 ns, while the exponential decay due to the dynamics has a time constant of order 1 µs, giving us a factor of 20 separation between the two time scales.

Static
Dynamic

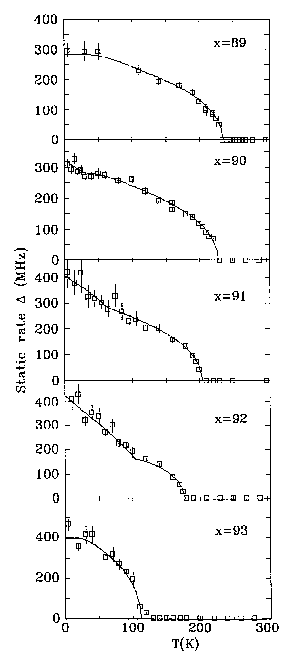
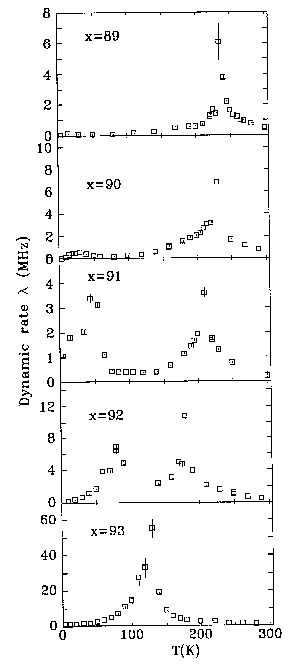
The data shown above for a-FexZr100-x demonstrate the power of µSR. Two magnetic transitions are clearly seen. On cooling from 300 K, the static signal (left panel) is zero until Tc is reached, then static magnetic order develops and the signal strengthens on further cooling. For x=90, 91 and 92, there is a break in the temperature dependence, with a marked increase occuring at a reasonably well-defined temperature. The dynamics (right panel) also reflect this behaviour. On cooling through Tc, the relaxation rate diverges. Below Tc, the relaxation slows as the static order develops. However for x=90, 91 and 92, we see a second maximum at the same temperature that the break in slope of the static order was observed.

Magnetic phase diagram for a-FexZr100-x

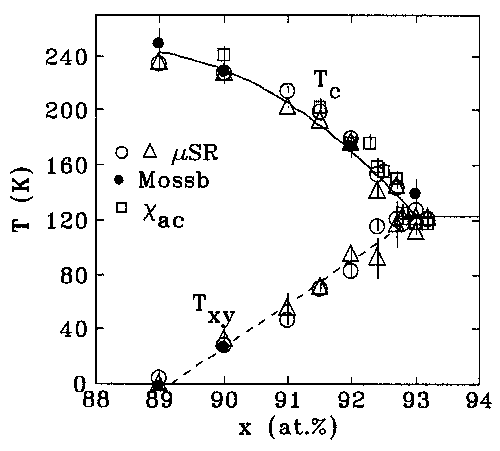
A complete analysis of the data is summarised above as a magnetic phase diagram.
The correspondance in Tc values determined from both static and dynamic µSR and also from more conventional methods confirms the validity of the approach. The similarly close correspondance between static and dynamic determinations of the second transition (Txy) confirms that a single transition occurs as expected from earlier experimental and theoretical work. The analysis also reveals that the entire volume of the sample is involved in both transitions, and that there are no isolated or superparamagnetic clusters present.
The high density of points around x=93 was used to determine that the critical concentration for the loss of ferromagnetic order in this system is x = 92.8 ± 0.1 at.%. No evidence for ``re-entrance'' (development and subsequent loss of a long-range-ordered state on cooling) was found in this, or any other system we have studied.

Comparison with Selective Excitation Double Mössbauer Spectroscopy
(SEDM)

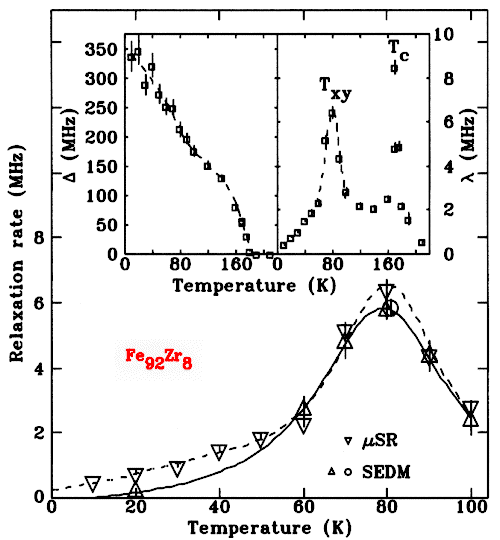
Relaxation rates derived from µSR and SEDM around Txy for a-Fe92Zr8.
Insets show the static (left) and dynamic (right) signals derived from µSR for both Tc and Txy.

The comparison between SEDM and µSR is particularly instructive. µSR is an interstitial probe that is affected by any fluctuations in its magnetic environment. By contrast, SEDM probes the behaviour of the iron moments directly, and is dominated by moment reversals. The almost perfect agreement in derived relaxation rates around Txy indicates that moment reversals are the dominant relaxation mechanism.

Field induced shift of Txy

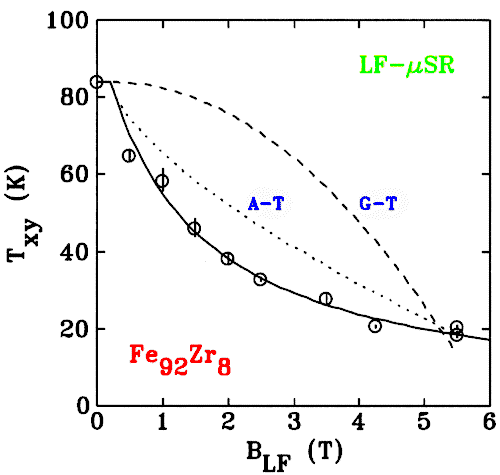
The effect of an externally applied magnetic field on Txy is shown here along with the predictions of two theoretical models (A-T and G-T). The gross mis-match between theory and reality is readily apparent.

Our early work on transverse spin freezing was carried out using Mössbauer Spectroscopy in an applied field. Comparison with µSR data showed that the Mössbauer derived transition temperatures were too low. We therefore repeated the µSR measurements with a longitudinal magnetic field applied to the sample and showed that it rapidly suppresses the transition.
As the figure above shows, the functional form of this suppression is not consistent with mean-field models of spin glasses. We are currently using numerical modelling to invistigate this effect.

a-(Fe1-xMnx)78Si8B14: a site-frustrated system.

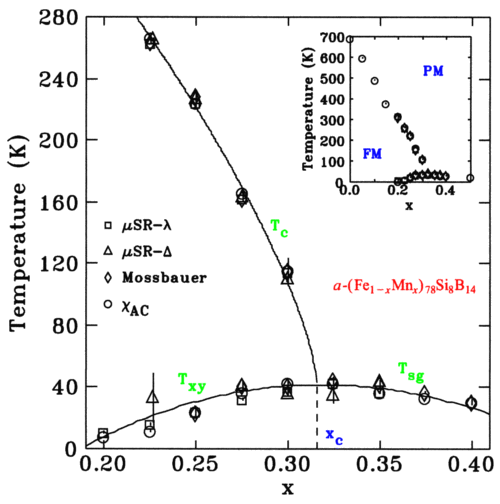
The magnetic phase diagram for a-(Fe1-xMnx)78Si8B14 derived from
bulk magnetic measurements and also from both µSR Mössbauer Spectroscopy
Inset shows full range of behaviour.

Following suggestions in the literature that this site-frustrated material exhibited two distinct transitions below Tc, we applied several techniques that probed both static order and dynamic fluctuations on a wide range of time scales. As the phase diagram clearly shows, all of the techniques agree within experimental error. There is only one transition below Tc, and this transition exhibits the same signatures observed at Txy in the bond frustrated a-FexZr100-x system. All static and dynamic signatures coincide.

For more details of these projects, see my recent publications page.

Some useful µSR web links:
Updated: 9/May/03
All photographs copyrighted by:
Dominic Ryan, ERP 425, (514) 398-6534