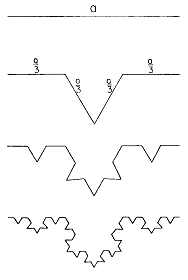
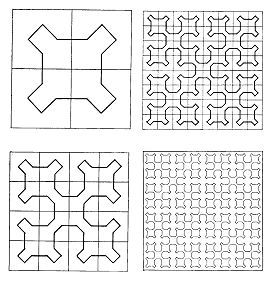
Fractal Sets:

Fractals are geometric sets of points (they are one or zero, black or white - we are on or off the set) which are invariant under "zooming" ("blowups"). Fractal sets became widely known in the 1980's largely as a consequence of Mandelbrot's 1983 book "The fractal geometry of Nature".

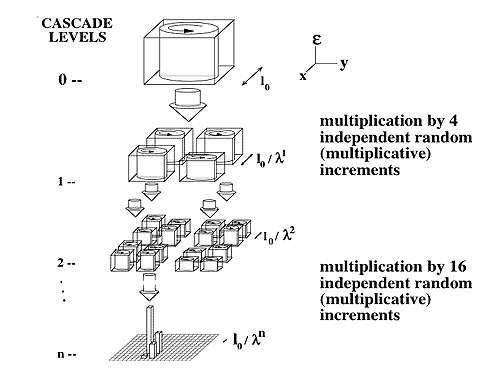
A fractal Koch curve ([Koch, 1904]), reproduced from [Welander, 1955] to illustrate the mixing of a two dimensional fluid. A fractal Peano curve, reproduced from [Steinhaus, 1960] showing how a line (dimension 1) can literally fill the plane (dimension 2), illustrating how streams can fill a surface.

 

Multifractal fields, measures:

Multifractals are the generalization required to deal with fields which have values at each point. Geophysical examples of geometric fractal sets are the set of points defined by the locations of meteorological measuring networks (Lovejoy et al 1986). Examples of multifractals include the earth's topography where each location has an altitude (Lovejoy and Schertzer 1990, Gagnon et al 2003), or the wind, or temperature fields. One can think of a multifractal as being composed of an infinite hierarchy of fractal sets; in the topography example, each line of constant altitude defines a different fractal with a different fractal dimension.

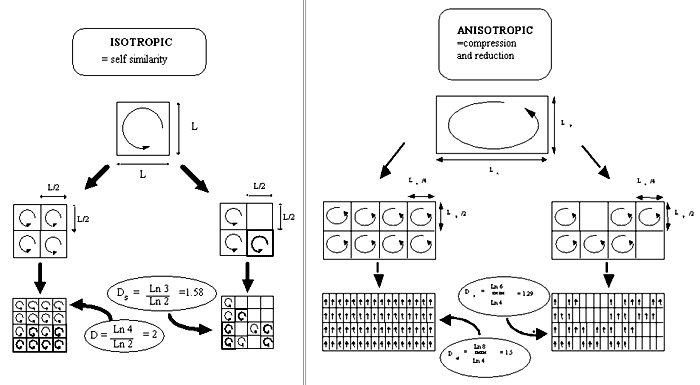
The generic multifractal process is the cascade. Discrete in scale multiplicative cascade processes (Yaglom 1966, Mandelbrot 1974) are also multifractal:

c(g) is a codimension (Schertzer and Lovejoy 1986) or a Cramer's function (Mandelbrot 1991). c is the difference between the fractal dimension of a set and the dimension of the space in which it is embedded (ex. a straight line in 3D space has c=3-1=2).

Anisotropic Mulitfractals:

Isotropic versus anisotropic cascades (schematic for the vertical cross-section of stratified turbulence):

Order of singularities:

A multifractal is a kind of superposition of singularities of many different orders. The order of a singularity g of the field e at the resolution l is the exponent:

ie how algebraically fast it diverges

g gives the scale independent characterization of the field.

  • high singularities
  • medium singularities
  • low singularities

 

Mathematically, multifractals are defined by two groups; one determines the statistics (or more precisely however they vary as a function of scale), while the second defines the notion of scale itself. On its own, each would be too general to be manageable/useful. Fortunately, each admits a significant simplication: for the statistics, "universal multifractal" (three parameters), for the definition of scale, "linear Generalized Scale Invariance" (in d dimensions, the most important paramters are the elements of a dXd matrix). Nonetheless, the range of possible behaviours is quite bewildering; the galleries here are aimed at giving a visual impression of what is possible.

next >