
| introduction
| multifractals
| clouds | topography
| topography perspective|misc
| movies | covers
| glossary |
publications |
 |
|
|
| introduction
| multifractals
| clouds | topography
| topography perspective|misc
| movies | covers
| glossary |
publications |
|
| | 1 | 2 | 3 | 4 | 5 |6 |
|
|
Effects of varying unit ball In polar coordinates, we can represent the unit ball by it's radius R as a function of angle theda; a simple parametrization is: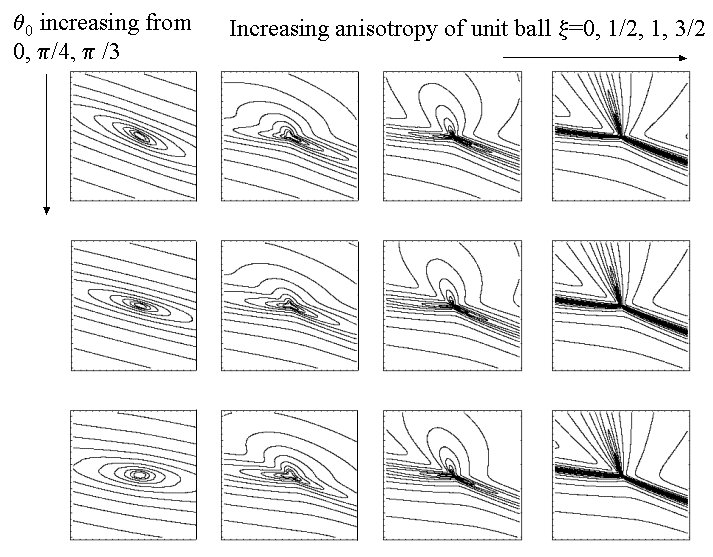
|
This site currently maintained by Eric DeGiuli, eric DOT degiuli AT utoronto DOT ca.